Another
problem I find with this experiment is the expectation itself. I decided
to study the effect on a very simplistic basis to understand the nature of
this second order effect. While my calculation method is longer than the
formula, it is simpler and retains the understandings of
the inner workings of the effect instead of relying on faith in
the correctness of a formula. The purpose of my site is
to communicate close to the level of laymen so that anyone examining it
can remain confident in the correctness of what is being
conveyed.
The reason
the reading is so very small in this experiment is
because of the fact that the light does not simply go with or against
the flow but it does both because of the reflection. Many people erroneously assume
that because the light is sped up in one direction but
then equally slowed down on the return trip that there is an exact cancellation.
This is not true of course and I've made some simple diagrams to help
understand the concept of this second order effect.
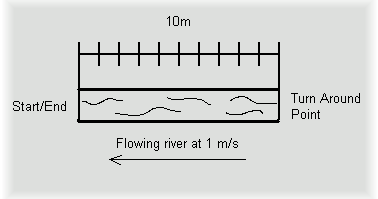
Imagine a swimmer that swims to one point
and back at a constant speed. In the chart below and even visualizing the
numbers yourself using the above drawing you can see how the effect
occurs. Additionally you can see how the effect decreases as the
difference between the swimmer speed and the river flow grows. Finally you
can see that length does not affect the relationship. The total time
travelling (and path length by the swimmer's estimation) grows by a
certain percentage based on the prior mentioned relationship.
| One
Direction path length |
10 |
20 |
| Swimmer speed |
2 |
2 |
| Flow |
1 |
1 |
| Norm
(no flow) |
10T/20L |
20T/40L |
| Swimmer's Est. Time (*speed = total 2-way
length) |
13.333 |
26.666 |
| Relation to Norm |
133.333% |
133.333% |
| One
Direction path length |
10 |
20 |
| Swimmer speed |
3 |
3 |
| Flow |
1 |
1 |
| Norm
(no flow) |
6.666T |
13.333T |
| Swimmer's Est. Time (*speed = total 2-way
length) |
7.5 |
15 |
| Relation to Norm |
112.5% |
112.5% |
| One
Direction path length |
10 |
20 |
| Swimmer speed |
6 |
6 |
| Flow |
1 |
1 |
| Norm
(no flow) |
3.333T |
6.666T |
| Swimmer's Est. Time (*speed = total 2-way
length) |
3.42857 |
6.8571 |
| Relation to Norm~ |
102.8% |
102.8% |
Now that I have established the
relationship, I can deal with the Earth's speed (flow) and the speed
of light (swimmer) in units of their relationship.
Earth's Orbital speed: 29.78
km/s
Light Speed: 299,792.458
km/s
10,066.906 to 1
| One
Direction path length |
100669.06 (x2 =
201,338.12) |
| Light
Speed (swimmer) |
10,066.906 |
| Ether
wind (Flow) |
1 |
| Norm
(no flow) |
20 |
| Actual
travel time (Swimmer's Est.) |
20.000000197350382813136543039538 |
| Relation to Norm |
1.0000000098675191406568271519769 |
trip1 -1 =
10.000993452551613337140243511116
trip2 +1 =
9.9990067447987694759962995284223
What does this all mean?
You can use the "relation to norm"
to determine how much longer the path length and/or travel time should be
in any MMX-like experiment if there was no such thing as entrainment. The
above examples show how distance can scale so long as the relation between
the swimmer and flow remain the same.
First we need
to examine the device used in the the original
MMX
to determine what is meant by path length. If you read the dimensions of the
device it is a 1.5m square. By looking at the drawing you can tell that
it, at least partially, traverses corner to corner 16 times. If it
was exactly corner to corner this would be almost 34 meters. We'll assume
that Dr. Michelson has some ability with measurements and only meant that
the one-way path was 11 meters but that the total optical path is actually
22 meters. This gives us 217.08 nm extra path
length along the direction
of the Aether wind. ("Relation to Norm" x Path Length)
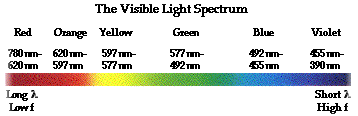
Repeatedly through the publication
of the MMX he mentions that they are using yellow light. (577-597
nm)However you'll also
find it mentioned in the original publication that a single turn of a
100 thread per inch screw moved "nearly 1000
wavelengths" of what he called
white light at that
point in the paper. This screw moved the mirror at the halfway point of the optical path so
1 turn would actually shorten the total path length .02 inch instead
of the immediate thought of .01. This would indicate the light
to be 508nm at 1000, or as much as 564nm at 900 wavelengths(which I think he
would have said directly) So this is slightly vague. Thankfully he goes on to clarify
further:
"Considering the motion of the earth in its orbit
only, this displacement should be 2Dx1.0e-8" (220 nm)Next he goes on to say that "The distance D was about 11 meters, or 2e+7
wavelengths of yellow light; hence the displacement to be expected was 0.4
fringe" This tells us with certainty that he believes his
light to be 550nm which
is actually green. However, the most important consideration that can tell
us for certain what the real wavelength of the light being examined in his white light
interferometer experiment was the fact that he used sodium light to line up the
fringe system! Since the sodium doublet (special double fringes from
sodium interferometry)resides at 589.0nm and 589.6nm and he
calibrated his interferometer with sodium light, the darkest fringe was set
for 589nm and this differs from his belief about the wavelength. (it's also
yellow instead of green) This means that his expectation of .4, while
close, is not quite right.
Instead the calculation comes out
to: 217.08nm less 1.34nm that the perpendicular path is modified by
aberration gives us a 215.74 path length difference. Divide the actual
wavelength of 589 that was used to calibrate the fringes and we have an
expected fringe shift of .366 We can
forgive his slightly incorrect assumption of a 550nm wavelength given
that it was 1887....
For those of you following Michelson's mathematical
path that would mean that D is 11 meters / 589nm. (18675721.562
waves) resulting in an expectation of a 0.368566 fringe shift without
aberration. (29.78^2 / 299,792.458^2) * 37351443.124 = 0.368566.
Aberration
This effect is
so small that I find it almost
unnecessary to write about but because Michelson mentions it at the
beginning of the paper, I will also. There is actually a
small effect perpendicular to the wind called aberration. However, because it is
only a second order effect it calculates to only about 1.34nm
extra path length. This should be subtracted from the expected path length difference for
ultimate accuracy but it can be ignored for the most
part.
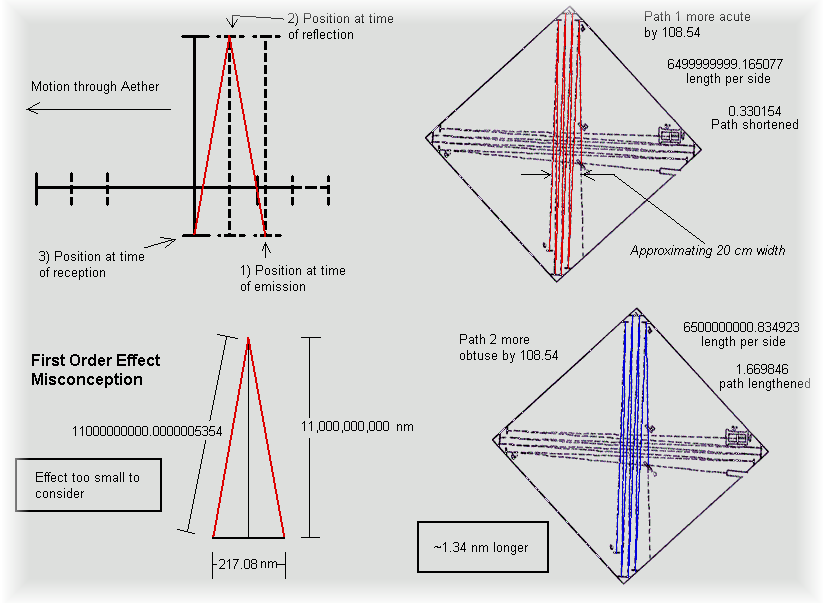
The above
figure should reveal the easy misconception on the left and the actual
effect on the right. The above drawing should suffice for puzzling it out
yourself. The important thing to remember is that the concept picture
Michelson represents at the beginning is misleading. The total path during
which aberration is happening goes both with and against the wind for the
round trip on the actual interferometer instead of the idealized concept.
The red path on the left in the above drawing is
propagating slightly into a headwind and the blue path below it is
propagating with a tail wind.
What
Was Actually Seen
A quick substitution of a few
numbers reveals the nature of what was actually detected by the
interferometer. Let's suppose that the differential speed we
expect between the earth and the ether is around one-third what
Michelson expected.
Earth's Orbital speed: 10.00
km/s
Light Speed: 299,792.458
km/s
29,979.2458 to 1
| One
Direction path length |
299,792.458 (x2 =
599,584.916) |
| Light
Speed (swimmer) |
29,979.2458 |
| Ether
wind (Flow) |
1 |
| Norm
(no flow) |
20 |
| Actual
travel time (Swimmer's Est.) |
20.000000022253001145832171615753 |
| Relation to Norm |
1.0000000011126500572916085807877 |
So, 24.4783nm
path length difference should have been the expected reading from this
assumption.("Relation to Norm" x Path Length) As you can see, this
is a little more than one-tenth the expected reading of
the MMX while the actual speed
is over one-third as large! 24.4783/589 = .04 of a
fringe
Or lets check another
similar number...
Earth's Orbital speed: 8.00
km/s
Light Speed: 299,792.458
km/s
37,474.0573 to 1
| One
Direction path length |
374,740.573 (x2 =
749,481.145) |
| Light
Speed (swimmer) |
37,474.0573 |
| Ether
wind (Flow) |
1 |
| Norm
(no flow) |
20 |
| Actual
travel time (Swimmer's Est.) |
20.000000014241920689623184063047 |
| Relation to Norm |
1.0000000007120960344811592031524 |
trip1 -1 =
10.000266858396952842169085573917
trip2 +1 =
9.9997331558449678474540984891303
So, 15.6661nm
path length difference should have been the expected reading from this
Scenario. ("Relation to Norm" x Path Length) As you can see, this is
still around one-tenth the expected reading of the MMX
while the actual speed
is still nearly one-third as large. 15.6661/589 = .027 of a
fringe...
If we look at
the number from the page which shows the properly temperature adjusted
numbers we get
the following readings of the screw head (using the full rotational
reading for consideration of the full period effect):
Day Median: 42.58125
Lowest
deviation from mean: 1.80125 (40.78)
Highest
Deviation from mean: .1.77875 (44.36)
Avg
deviation: 1.79 of a screw head division
Night Median: 50.863125
low: 1.663125
(49.20)
high: 1.686875 (52.55)
Avg
deviation: 1.675
Final Avg: 1.7325
In consideration that a single number on
the measurement device represents an average .02 (.025 - .0166)
of a fringe/wavelength, .03465 of a fringe is what was
detected. Slightly less than 10 km/s is what the original
MMX detected.
A Null Result
To actually qualify as a null
reading it would have to be below 5% of the expected wind speed,
so let's examine that now:
Earth's Orbital speed: 1.489
km/s
Light Speed: 299,792.458
km/s
201,338,118.2 to 1
| One
Direction path length |
2,013,381,182.0 (x2 =
4,026,762,364) |
| Light
Speed (swimmer) |
201,338,118.2 |
| Ether
wind (Flow) |
1 |
| Norm
(no flow) |
20 |
| Actual
travel time (Swimmer's Est.) |
20.000000000000000493375960986189 |
| Relation to Norm |
1.0000000000000000246687980493095 |
trip1 -1 =
10.00000004966769402172595661881
trip2 +1 =
9.9999999503323064716500043673796
In this case you have a grand
total of 0.00000054271nm extra path length or a 9.214e-10 of a fringe
shift. Only readings smaller than this can be considered
truly null by typical standards.
The Variation of the
Readings
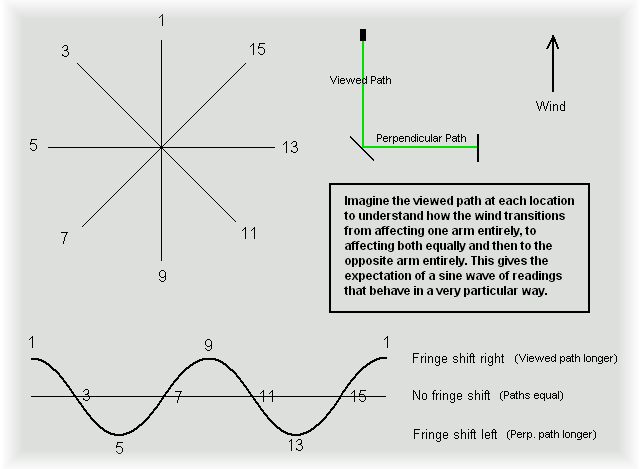
Another expectation that is not discussed
in the relativistic community is the way the readings would change as the interferometer was
turned in a full circle if there was an ether wind. This is
a very outstanding behavior because it is a half period effect. This means that a
full iteration of some cyclical event happens in only one half turn of the
device. The wind was
expected to cause the readings to both instead peak and trough twice during one full
rotation.
As you can see above, as both arms of the interferometer are at
some variation of 45 degrees to the wind, both paths are affected equally,
bringing the fringes back to the center. The
expectation of this behavior is likely the single most important
fact to understand when considering the implications of
Michelson's and Miller's results. Both of them had this very distinct
pattern even after averaging many many readings together. This cannot be
mistaken for random error in readings or errors in the device. (But I
suppose I've found that faith can always find a way
to twist simple fact)