Twins Paradox

This is most obvious of all the varying paradoxes that arise from relativity because almost every human on earth has some ability with logic. If we know that speed is only relative between 2 reference points and there is no universal or third reference point, then we know that one point moving is exactly the same as the other point moving. Let me illustrate.

I've found a site that has some really fantastic explanations and diagrams of the relativistic side of the story here.  I've taken the liberty of fiddling with some of his excellent images and even directly copying some text.

Red and Blue construct identical clocks, consisting of a light beam which bounces off a mirror. Tick, the light beam hits the mirror, tock, the beam returns to its owner. As long as Red and Blue remain at rest relative to each other, both agree that each other's clock tick-tocks at the same rate as their own In relativity. if there is any motion between the two then relativity says one will run faster and the other slower.

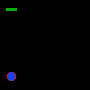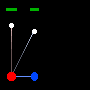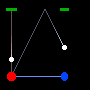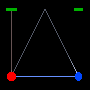The paradox lies in trying to pick which is travelling and which is still. If you examine the two images to the left you'll see that though this is a rocording of the exact same event, it is from two different perspectives. In one case we decide that Red is "still" and in the other case we decide Blue is. We usually make this arbitrary decision based on who we are following along with but both views are equally valid in physics. One view is not more correct than the other and selecting one view, such as the earth, as the standard is not valid. This is known as Galilean relativity. (which I do not question btw) If the speed of light is constant, then why is it that from each stationary view the traveller's beam seems to travel further in the same period of time? The concept of time dilation came from trying to resolve this problem.

If we examine just one view, (lets use the top image) we could say that time must be going by slower for Blue because for light to travel that far it would take a longer period of time. If you must accept that light always travels the same speed and that it travelled further then you must conclude that what seems simulataneous from Red's view must not be simultaneous for Blue. This is not my logic friends, I'm just explaining the relativists logic.

Unfortunately, you must stop your thinking there for it to make any semblance of logical sense. If you continue on to think about it and examine it from Blue's view, you will conclude a completely opposite effect. From Blue's view, time must be going by slower for Red. Both views connot be correct

So the question remains which one is moving and which is stationary without a universal reference frame? In the Twins paradox example, one twin stays home and the other travels away and then back and the traveling twin ages less. Most explanations usually give you some more complex equation or explanation about one side of it and then forget to do the same to the other side and get the paradox again. Lets go back to this excellent sourcehosted by the university of colorado.

On his dilation page he casually explains that the paradox is taken care of with a diagram explaining simultaneity (actually the lack thereof).  In his light cone diagram page he goes on to explain how time is skewed in the other plane from each of the perspectives and something that seems like it happens at the same time in one does not in another. Has anyone other than me noticed that we've not resolved whose clock will be slower when the two meet up again?

There is one other explanation that is more difficult to recognize as logically faulty that I will try to cover now. Supposedly the deceleration and acceleration of the traveling twin is the point at which the other twin's age must be calculated. First and formost, the twins paradox is only one simple example of Dingles Dilemma and acceleration is not required at all for the paradox to arise. Here's a quote from his book, Science at the Crossroads:

According to the theory, if you have two exactly similar clocks, A and B, and one is moving with respect to the other, they must work at different rates (a more detailed, but equally simple, statement is given on pp. 45-6, but this gives the full essence of the matter), i.e. one works more slowly than the other. But the theory also requires that you cannot distinguish which clock is the 'moving' one; it is equally true to say that A rests while B moves and that B rests while A moves. The question therefore arises: how does one determine, consistently with the theory, which clock works the more slowly? Unless this question is answerable, the theory unavoidably requires that A works more slowly than B and B more slowly than A --which it requires no super-intelligence to see is impossible.

If two bodies are moving relative to eachother, they both believe themself still and calculate the other's clock as running slower. When they pass eachother, which clock recorded more time? The acceleration explanation  is a perfect example of a non-reality related mathematical model. Someone using this explanation is looking at a triangle on a sheet of paper and doing Pythagorean theorem calculations without examining if that mathematical model is reflective of reality and can actually be used to solve the problem or not. Like a grade-schooler with a word problem; though he's got a calculator and uses an equation very useful and appropriate in other situations and even comes up with the right answer for the equation he decided to use, he still has solved the problem incorrectly. He's used the wrong equasion because his logic failed. Take a look at the acceleration excuse here.

Subsequently this acceleration explanation also means that only the change of reference frames causes time dilation, not the actual speed itself. That would then mean that regardless of the time traveled at a higher rate, the two frames would always be off by a certain amount because the acceleration is a constant. This explanation lacks internal consistency. What if the path of the traveling twin was a circle? What if a wormhole turned him around? So it isn’t speed, it’s simply changing reference frames that causes time differences eh? Ohhhh, then that must be the reason my vibrating massager’s battery runs out so quickly! All that reference frame changing! Hmmm, but what about all the relativity needed in the GPS satellites and Hafele-Keating?! (atomic clocks in planes) Don’t worry, that’s covered in the experiments section.

The impasse is that the proponents of this explanation are saying that time dilation is not occurring because of travelling at a given speed it is only the transition that is the cause. If this is true then it does not matter how long the traveling twin is moving at the extremely great speed, only that the change in reference frames is causing the dilation. For example, according to this explanation, if a twin traveling at 99.9998%C did so for five years, the age difference between himself and the stationary twin (lets say 20 yrs) would be equal to the age difference if he traveled at 99.9998%C for only 1 second. They cannot use traveling at a rate for set time as any part of the equation or the twins paradox comes back. The only other option is for them to insert "proper time" which is an arbitrary universal reference frame and breaks down the entire argument.

This now leads to another problem. If acceleration all by itself causes time dilation we really have some interesting things that would be happening. There is no difference between acceleration and deceleration if there is no universal reference frame. If you use an accelerometer you will find that deceleration is just acceleration in the opposite direction and it is inconsequential that you accelerated previously to get to your current reference frame. Additionally, by their explanation, it would not matter if you only accelerated half the total speed, cruised for a year, and then accelerated the rest of the way. The accelerations would be additive. Now consider for a moment all the car and plane rides in your life. Heck, consider all the times you walked to the fridge for a snack. Add your lifetime's accelerations together and, though I haven't tried to calculate it, I think we can be fairly certain you'd make it to lightspeed pretty quickly. Maybe that's why active people live longer huh? LOL