Relative Primer > Part 2
- A Moment of Review -
Before we continue, this is a good point to stop and think all of this through and really make sure you
understand exactly what is going on. Make sure you are in the mind of Lorentz before you move forward or
you cannot come to the same conclusions.
Remember:
- Lorentz believes in a physical world that is a clockwork mechanism with absolutely zero spooky effects.
- He believes that there is an ether that is perfectly at rest and all moving objects can be compared to it.
- He believes that light only travels at its normal speed in relationship to the ether rest frame.
- He is (and you are) attempting to explain why a moving interferometer wouldn't detect its own motion.
If you travel on a train at 1 MPH less than the speed of a bullet as someone fires a shot along-side of you, then
you would be able to look out your window and see the bullet slowly passing you, but you would measure it as travelling at only 1 MPH!
Lorentz believed the same was true of light because it had to travel through the stationary ether. Using
the same analogy, the ground and air, are the stationary rest frame (the ether) and both the bullet (the light)
and we in our train (the interferometer) are travelling together through it but at different speeds.
Since on a moving interferometer, light would seem to go slower upstream or upwind... or it would have to
"cover more ground" before hitting the upwind mirror, we are assuming that the
wind itself must shorten the measuring object just enough to eliminate that "extra ground".
- An Alien Perspective -
Consider the following situation:
An alien species which lives in the vacuum of space determines to study sound in an atmosphere. They are incapable of surviving in an atmosphere so they use certain experimental devices to study mechanical waves in a medium (EG sound). In one of their first experiments they placed two sound reflecting surfaces at right angles from an emitter approximately ten feet from the emitter. These surfaces are held away from the emitter by the only building material they have access to which is also somewhat spring-like. They placed this assembly on a flatbed truck with the emitter at the tail end. It is arranged so that one sound reflective surface is closer to the front of the truck by ten feet and one surface is placed perpendicularly to the truck's axis, displaced from the emitter by ten feet. The experiment is placed at an elevation at which sound travels 1 foot per millisecond to simplify calculations.
The emitter is also a receiver that can only determine whether or not the sound reflected from each of the reflecting surfaces arrives at the same time or at different times and by how much the arrival times are displaced. Given what they know about wave mechanics so far, they determine that if the truck is put in motion, the waves will arrive at different times. Using this expected displacement, they believed they would be able to determine how fast the truck might be moving at any given time. They also believed that if there was a headwind they would be able to determine that as well since the motion of the truck was already known and they were pretty sure there was an awful headwind the truck was going into.
Unfortunately, after putting the truck in motion there was zero difference in the arrival times of the echos from the reflectors. No matter what speed the truck moved they both arrived back at exactly the same time and this was highly confounding to all their notions about the way waves in an atmosphere behaved.
(These images will be explained in greater detail later)
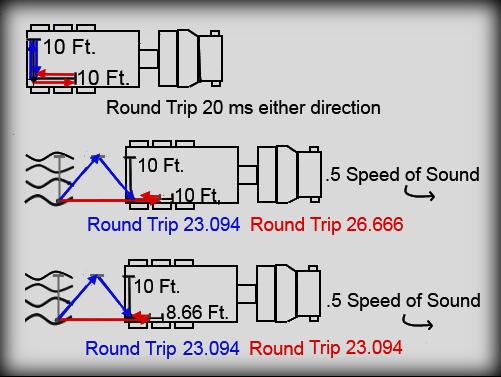
Thankfully, one of their respected scientists, Egeorg Gitzflerad, suggested it was the nature of their materials that was the cause. He believed that perhaps the wind was always just the right strength to cause the forward mirror to be scrunched toward the emitter just the right amount to make up for the expected difference.
Another scientist, Kehndri Orlzent, was fascinated by this development in their understanding of sound waves. He decided that it would be important to mathematically represent this concept of Gitzflerad's for the scientific community.
After some consideration of the experiment and some calculations, he figured out that the crosswind path would always be a certain angle away from perpendicular for a certain speed. This was true regardless of the distance away the crosswind mirror is placed. It could easily be represented like a graph. If the speed of the vehicle was half the speed of sound then whatever angle would allow the crosswind to be double the length of the experiment's motion would always be the angle of the spherical sound wave captured by the crosswind mirror.
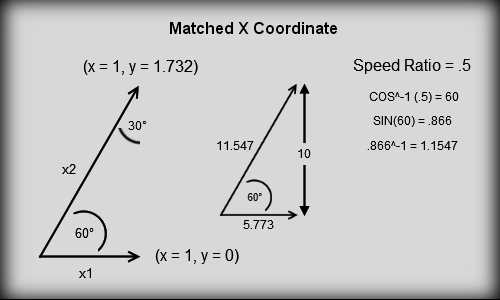
- A Simple Geometry Problem -
Said another way, for every speed there is a right triangle that is created. If the experiment is put in motion from left to right, the path of first crosswind reflection makes a right triangle. This triangle can be envisioned with the hypotenuse on the left side with the other two legs on the x and y axes. The length of the hypotenuse will always be a length in proportion to the experiment's motion which is equal to the relationship between the speed of sound and the motion of the vehicle. This invariably creates a particular angle.
What is so interesting is that, with this angle defined, the problem can now be discussed and explored in terms of Pythagorean theorem and/or trigonometry. This means that there will be only one point at which a single wave will return to the source after traversing the crosswind.
Orlzent knew that we now have a known target quantity that the upstream or co-wind path length must be shortened by and it will always be related to the relationship between the speed of the experiment and the speed of sound. Just as sin, cosine and tangent are formulas that represent relationships between the sides of a triangle, there are derivatives of these that can also represent relationships between sides. This was Orlzent's first discovery of what would later be called gamma.
The way he discovered this was through the realization that a simultaneous arrival time could be reached by either shortening the upwind arm of the experiment or lengthening the crosswind arm. In considering our truck experiment at .5c (the speed of sound), this means that we can cause the path lengths to match by either lengthening the crosswind path or shortening the co-wind path.
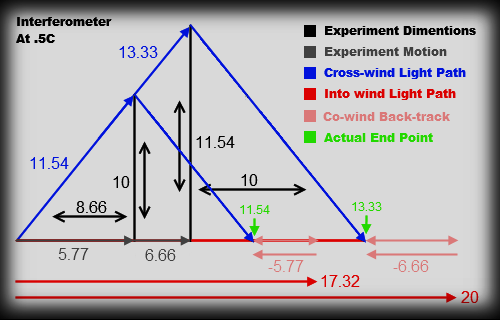
Method 1: Simply find the ratio of the growth rates between the path traveled upwind and the path traveled cross-wind. In specific numbers, this means that the up/downstream sound path would take 26.666 seconds to traverse if the distance between the emitter and mirror remained 10. But because there is only one angle light will traverse, there is one particular distance the cross-wind path will be: 23.094. (how to find this will be explained further in method 2) Both of these path lengths grew larger than stationary, but at different rates. The relationship between their growth rates is 23.094/26.666=.866 So if we always want them to match, the cross-wind must be reduced by the difference of growth rates. The co-wind must be shortened by the amount it would otherwise gain beyond the cross-wind. This solution is useful for a single speed but does not provide a deep enough understanding yet to create a transformation for all speeds.
Method 2: Once again we consider that the up/downstream sound path would take 26.66 seconds to traverse if the distance between the emitter and mirror if the path remained 10. Using trigonometry and the principles established above we can easily find the length required for the crosswind leg of the experiment to achieve simultaneous arrival.(how much it would have to be extended) Using the simple calculation of cos^-1(.5) gives us the angle of 60 degrees. We know that during the total up/down that the sound travels, the experiment travels half that distance because it travels .5c. This means that when sound travels 26.66, the experimental equipment (the truck) only travels a grand total of 13.33. We also know that we can represent the motion of the experiment and the motion of the crosswind path as two right triangles. So basic geometry tells us that if we want the reflection point we must cut the experiment's motion in half to represent one right triangle. (see Equal Triangles above)
We now have a hypotenuse that is at a 60 degree angle and the x axis leg is 6.66 and the crosswind path is 13.33. It is simple to find that the sine of 60 is .866 and we multiply that by the hypotenuse to find the “opposite” (y axis) leg would have to be 11.54 long. This means that the crosswind leg would have to be 11.54 long for the arrival time to be simultaneous if the upstream/co-wind leg remained 10 long.
Method 3:
Note: Method 2 must usually be discovered before method 3 can be easily understood. This is because it is more difficult
to predict the length required of the upstream leg without having a specific target because there is an upstream and downstream component that cause some
unexpected cancellation.
Using the same principles discussed, we know that, though the length of the crosswind arm is set at ten feet, the angle
at which sound will be reflected at .5c is still (cos^-1(.5)) 60 degrees. To find half the total crosswind path length for
a 10 long crosswind arm, we can solve for the other dimensions in a number of ways:
A) Tangent(60) = “opposite” over “adjacent”
gives us 1.732 which means that the length of the y axis leg is 1.732 times as long as the x axis leg. (10/1.732=5.77) Which
we can use with the shortcut that the hypotenuse is 2x as long at .5c giving 11.54 and a total path length of 23.09
B) We know that the sine of 60 (opposite/hypotenuse) is .866 therefore hypotenuse/opposite = .866^-1 = 1.154 so if the
crosswind leg remains 10 long, the hypotenuse = 11.54 and the total path length traveled by the crosswind is 23.09
Given this truth of a 23.09 crosswind, and because the experiment is traveling half the speed of sound, it will travel half as far for a total of 11.54 feet along it's path
of travel (x axis) when the crosswind reflection is received.(refer to "equal triangles" diagram above) From this point there are
numerous trial-and-error methods of arriving at the length the co-wind arm must be shortened to but let us instead focus on
a deeper understanding of the problem from a variety of viewpoints instead of just the solution. This is part of the process of
obtaining the understanding required for creating a transformation.
- Understanding the Implications -
If you know SR, you already know we must shorten the co-wind by gamma (.866) but your foreknowledge is cheating. It is very interesting and entertaining to find that when we invert the percentage of the path's growth along the crosswind path (from 20 to 23.09 = 1.154) we find that the amount the co-wind must be shortened to arrive at the same location. It is very similar to Pythagorean theorem. But how do we first make that leap of understanding without a process of trial and error? It is the equivalence of the triangles created by either lengthening one side or shortening the other that first gives the clue that shortening is precisely the inverse operation of lengthening.

"Gamma" is actually a simple relationship of growth patterns. Though average is not the proper term, it is “like” the average of the up and downstream (speed-up and slow-down) components after they are combined. For instance, gamma*gamma will give the total distance light must travel along the x axis if the length of the x axis arm is not altered. In our experiment at .5c if the sound had to travel all the way upstream and back down the 10 foot length the total path length would have been 26.66 instead of 20 and we can easily see that 1.154*1.154=1.333 which is the total growth of an unaltered co-wind path.
The angle of the crosswind is a representation of how much of the full (unshortened) growth pattern the crosswind is subject to. Notice that when we attempted to grow the crosswind to match the co-wind, we found that crosswind had to be lengthened to 11.54 to equal 1.33. (IE from 20 to 26.66) These two numbers are different at every speed but gamma*gamma will always arrive at the distance a wave would have to travel along the x axis if the experiment was not shortened.
Notice that the co-wind leg bears 100% of the effect of the wind (both sped up and slowed down) during it's traversal. The crosswind path is only partially affected by the wind because of its angle. However, as the experiment goes ever faster and the crosswind path remains the same length, the angle flattens out and the crosswind bears more of the wind's effect.
Why we have a gamma^2 final number is because the relationship explored is like one leg of a right triangle compared to the other leg doubled. IE the relationship in this case is like the relationship between the leg we've been calling opposite (y axis leg) and the one we call adjacent.(x axis travel) But we must duplicate the right triangle to consider the whole path length and then consider the relationship between the single “opposite” and the duplicated “adjacent”. It is a consequence of triangular relationships like Pythagorean theorem. More specifically, the reason gamma^2 gives us the unshortened path is because gamma is a squared relationship because the sides of a right triangle are a squared relationship. However, the reason gamma^2 is a result of Pythagorean theorem can be discussed more fully another time.
It is also interesting to note that as the speed of the experiment grows, the angle at which the crosswind travels flattens out in the same direction as the x axis travels. This causes the relationship between the legs of the triangle to change because “opposite” stays the same while “adjacent” grows. This gives us the strange non-linear changes we see in gamma at different speeds.
Finally gamma becomes infinite when the experiment reaches c because neither path can ever complete the trip. Neither path can ever reach the first mirror. (C is the universal speed limit in relativity because of what is equivalent to a divide by zero error)
- Summary -
The relationship between the movement of the experiment and angle of the crosswind path is a direct consequence of the relationship between the speed of the experiment and the speed of sound. IE:If sound travels 2x as fast as the experiment, the crosswind leg will be 2x as long. It is like a graph.

Therefore the angle created is a representation of two differing growth rates. The sine of the angle is another representation of that relationship. By using the sine of the angle, we can represent how much one side of a triangle must grow or the inverse to determine how much another side must shrink while maintaining the same triangle.
Gamma is a geometric representation of a relationship of growth rates. It is the result of solving the Michelson-morely experiment in a medium. The numbers and relationships represented by it do not exist if the wave travels as a constant with respect to a moving observer.
This is why gamma(inverse) can always easily be found on a scientific calculator by simply finding: SIN(COS^1(decimal of light speed))
(Go ahead, lean back. Take a nice deep breath and whisper “wow”)
- Conclusions -
The Lorentz transformation is designed as a mathematical illusion for light traveling in a medium. An observer who is ignorant of the wind will not be able to detect the wind and will mistakenly measure C as a constant at all speeds if they use the experimental setup described earlier with its ability to be "scrunched" by the wind.
This set of calculations therefore does not rely upon frame-independant “constancy” of the wave's speed but in fact depends upon the opposite to create the illusion of frame-independant “constancy”. This is a critical difference between Lorentz and Einstein.
Clocks which rely upon the transmission of the wave in the above experiment will be slowed by gamma because this is the amount of additional space the wave must traverse in one round trip, thus both length contraction and time dilation are incorporated in a purely mechanical wave model. (not frame-independently constant) IE: If atomic clocks and biological processes are governed by EM interactions, time will be perceived at a different rate for a moving observer in this purely mechanical model.
On the next page we'll discuss what your new logical understanding of relativity means in a broader context. What is the difference between this simple mechanical theory and the magic of Einstein's relativity?